Functions
RDM Fast Fourier Transform (FFT) APIs
RDM C/C++ API Reference
Collaboration diagram for RDM Fast Fourier Transform (FFT) APIs:

Functions
RDM_RETCODE rdm_fftInit (RDM_FFT *fft, uint32_t N, RDM_FFT_DIRECTION direction, RDM_FFT_DATA *workData, RDM_FFT_DATA inData[], RDM_FFT_DATA outData[])
Initialize an FFT object. More...
void rdm_fftTerm (RDM_FFT *fft)
Terminate an FFT object. More...
void rdm_fftCompute (RDM_FFT *fft)
void rdm_fftScaleIn (RDM_FFT *fft, double scale)
Scale the input of an FFT computation. More...
void rdm_fftScaleOut (RDM_FFT *fft, double scale)
Scale the output of an FFT computation. More...
void rdm_fftGetAbsPositive (RDM_FFT *fft, double threshold, double outAbsData[])
Get the absolute values of the positive frequencies of the output FFT. More...
void rdm_fftGetAbs (RDM_FFT *fft, double threshold, double outAbsData[])
Get the absolute values of the output FFT. More...
void rdm_fftSetReal (RDM_FFT *fft, double inRealData[])
Set the real parts of the input FFT. More...

Detailed Description

Fast Fourier Transform (FFT) is a class of algorithms for Discrete Fourier Transform (DFT). If you are unfamiliar with FFT, we would recommend the following resources:

The first resource above is a short visual presentation. The second resource is a lecture series from Stanford University. Discrete Fourier Transform (DFT) is introduced in Lecture 19. We would recommend that you watch a few of the first videos in this series then skip to 19-21 and finish off with 22.

Other resources to better understand the output of an FFT and its limitations and applications can be found here:

The implementation in RDM is inspired by the implementation described here:

Writing a good FFT algorithm is advanced art. RDM has a simple, reasonably efficient algorithm that requires the size of the data to be a power of two. If a more general solution or higher performance is needed, we suggest FFTW:

If you were to combine RDM with FFTW, please be aware that the license for RDM is incompatible with the free software license for FFTW. You will need a commercial license:

Function Documentation

rdm_fftCompute()

void rdm_fftCompute ( RDM_FFT * fft )

#include <rdmfftapi.h>

Compute the FFT

Call rdm_fftInit() before calling this function. The number of input data points and the number of output data transformed must have the length specified by the call to rdm_fftInit().

The input and the output consist of a number of complex numbers that are set up by calling rdm_fftInit().

An FFT of size N has an input with N samples (0 ... N-1) of a signal over a time period T that produces an output of size N (0 ... N-1) giving the DC level (0th element) followed by the energy for the frequencies (1/T, 2/T, 3/T, ... (N/2 - 1)/T), the Nyquist frequency ((N/2)/T), and lastly the energy for the negative frequencies. The upper half of the output array is often discarded when the output is analyzed. However, the upper part is needed for doing an inverse FFT (RDM_FFT_BACKWARD).

The Fast Fourier Transforms provided here are not normalized. It means a forward operation followed by a backward operation will result in the original data scaled by N. Some algorithms provide normalization by dividing the final results of a backward operation by N while other algorithms provide normalization by dividing the final result of both operations by sqrt(N).

Parameters
fft [IN] The FFT object to use for computing the addition

rdm_fftGetAbs()

void rdm_fftGetAbs ( RDM_FFT * fft,
double threshold,
double outAbsData[]
)

#include <rdmfftapi.h>

Get the absolute values of the output FFT.

This assumes an already computed FFT in the output, and here we will compute the absolute values. The output array must be the same size as the number of data points (N) as passed to rdm_fftInit().

Parameters
fft [IN] The FFT object to use for computing the addition
threshold [IN] Any data smaller than the threshold will be set to 0.0
outAbsData [OUT] The absolute values

rdm_fftGetAbsPositive()

void rdm_fftGetAbsPositive ( RDM_FFT * fft,
double threshold,
double outAbsData[]
)

#include <rdmfftapi.h>

Get the absolute values of the positive frequencies of the output FFT.

This assumes an already computed FFT in the output, and here we will compute the absolute values for the DC offset followed by the positive frequencies. The output array must be the same size as half the number of data points plus one (N/2+1) as passed to rdm_fftInit().

Parameters
fft [IN] The FFT object to use for computing the addition
threshold [IN] Any data smaller than the threshold will be set to 0.0
outAbsData [OUT] The absolute values

rdm_fftInit()

RDM_RETCODE rdm_fftInit ( RDM_FFT * fft,
uint32_t N,
RDM_FFT_DIRECTION direction,
RDM_FFT_DATA * workData,
RDM_FFT_DATA inData[],
RDM_FFT_DATA outData[]
)

#include <rdmfftapi.h>

Initialize an FFT object.

Initialize the FFT object. Use this function before calling rdm_fftCompute(). When done, make sure to call rdm_fftTerm().

The number of data points must be a power of two. Some algorithms for FFT allow any number of data points. Such algorithms are generally slower. With RDM, we have optimized for speed and simplicity.

The input, output, and work buffers consist of a number of complex numbers. These buffers are set up here and used when calling rdm_fftCompute(), rdm_fftScaleIn (), rdm_fftScaleOut(), rdm_fftGetAbsPositive(), rdm_fftGetAbs(), and rdm_fftSetReal().

Parameters
[in] fft The FFT object to initialize
N [IN] The number of data points. This must be a power of two
direction [IN] The direction
workData [IN] Work data used by the FFT. The length must be at least N/2 elements
inData [IN] Input data used by the FFT. The length must be N elements
outData [IN] Output data used by the FFT. The length must be N elements

Referenced by RDM::TIME_SERIES::fft_rdm< N, RANGE_T, INDATA_T, NEXT >::init().

Here is the caller graph for this function:

rdm_fftScaleIn()

void rdm_fftScaleIn ( RDM_FFT * fft,
double scale
)

#include <rdmfftapi.h>

Scale the input of an FFT computation.

This assumes that the FFT has not been computed for a given input, and here we will scale the input by the scaling factor given.

Call rdm_fftInit() before calling this function. The number of input data points and the number of output data transformed must have the length specified by the call to rdm_fftInit().

Parameters
fft [IN] The FFT object to use for the scaling
scale [IN] The scaling factor

rdm_fftScaleOut()

void rdm_fftScaleOut ( RDM_FFT * fft,
double scale
)

#include <rdmfftapi.h>

Scale the output of an FFT computation.

This assumes an already computed FFT in the output, and here we will scale that result by the scaling factor given.

Call rdm_fftInit() followed by rdm_fftCompute() before calling this function. The number of input data points and the number of output data transformed must have the length specified by the call to rdm_fftInit().

Parameters
fft [IN] The FFT object to use for the scaling
scale [IN] The scaling factor

rdm_fftSetReal()

void rdm_fftSetReal ( RDM_FFT * fft,
double inRealData[]
)

#include <rdmfftapi.h>

Set the real parts of the input FFT.

Call this before computing the FFT, and real input will be set according to the data provided. The imaginary part will all be set to 0. The input array must be the same size as the number of data points (N) as passed to rdm_fftInit().

Parameters
fft [IN] The FFT object to use for computing the addition
inRealData [IN] The absolute values

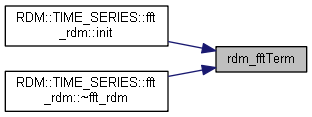
rdm_fftTerm()

void rdm_fftTerm ( RDM_FFT * fft )

#include <rdmfftapi.h>

Terminate an FFT object.

Parameters
[in] fft The FFT object to terminate

Referenced by RDM::TIME_SERIES::fft_rdm< N, RANGE_T, INDATA_T, NEXT >::init(), and RDM::TIME_SERIES::fft_rdm< N, RANGE_T, INDATA_T, NEXT >::~fft_rdm().

Here is the caller graph for this function: